L’analyse d’une enquête de satisfaction intègre fréquemment une matrice importance-satisfaction destinée à synthétiser les résultats de l’étude et à dégager des priorités d’action. Cette matrice présente généralement en abscisse le niveau de satisfaction de chaque critère et en ordonnée l’importance de ces critères. Le mapping ainsi généré met en évidence les actions essentielles à mener qui doivent porter avant tout sur les critères peu satisfaisants mais très importants, donc ceux qui se situent dans la partie en haut à gauche du graphique. Souvent, les donneurs d’ordre demandent des précisions sur les modes de calculs. Faisons le point sur les différentes méthodes possibles.
Le succès des mappings importance-satisfaction tient à leur apparente simplicité. En effet, le positionnement des critères sur un plan élémentaire en 2 dimensions « parle » à tout le monde. Le commanditaire y découvre un résumé efficace des résultats recueillis avec un plan d’action explicite et facile à communiquer. Les personnels sur le terrain identifient immédiatement les leviers de progrès à actionner en priorité ainsi que les points forts actuels qui nécessitent une vigilance maintenue. La représentation peut d’ailleurs être encore simplifiée si on présente le mapping découpé en quatre quadrants avec, dans chacun une liste des critères par ordre d’importance plutôt qu’un positionnement précis en fonction des coordonnées.
Cette apparente simplicité masque en réalité une complexité sous-jacente qui, lorsqu’on en est conscient, incite à s’entourer de quelques précautions dans l’interprétation des résultats. En effet, plusieurs méthodes existent qui peuvent, en partant du même jeu de données, proposer des répartitions différentes des critères. Toutes les matrices importance-satisfaction se ressemblent, mais chaque méthode calcule les coordonnées à sa façon. Une même méthode peut également proposer plusieurs répartitions des résultats selon les paramètres définis par le chargé d’étude. Il convient donc de mieux connaître les méthodes utilisées pour mieux exploiter les résultats qui en découlent.
La méthode déclarative
Le moyen le plus direct pour évaluer le niveau d’importance que les répondants accordent à chaque critère est de le leur demander. Certains questionnaires doublent donc les questions de satisfaction d’autant de questions d’importance. Le répondant indique généralement sur une même échelle en 4 points ou avec une notation sur 10 l’importance de chacun des critères proposés, puis sa satisfaction par rapport à ces critères. Il suffit ensuite de calculer pour chaque critère la moyenne des notes d’importance (directement ou en affectant une pondération aux différents points de l’échelle) et celle des notes de satisfaction pour obtenir les coordonnées de projection sur le mapping.
Cette méthode à l’apparente simplicité a plusieurs inconvénients
rédhibitoires :
- Le fait de doubler les questions alourdit considérablement le
questionnaire et le rend indigeste aux répondants. De nombreuses
recherches ont mis en évidence une très forte influence de la durée du
questionnaire sur les taux de réponse et la qualité de ces réponses. En
rallongeant et complexifiant ainsi le questionnaire, on augmente donc le
risque d’abandon en cours et de réponses approximatives.
- Si la notion de satisfaction correspond à un sentiment, la notion
d’importance fait, elle, davantage appel à la réflexion. Les
répondants ont tendance en la matière à rationaliser leurs notations en
privilégiant des dimensions logiques (prix, disponibilité des produits…)
au détriment de critères plus subjectifs que l’on pourrait
considérer comme secondaires à la réflexion mais qui peuvent contribuer
très fortement au sentiment de satisfaction ou d’insatisfaction
(propreté, décoration, ambiance sonore…). Cette situation génère des
biais et peut conduire à une mauvaise orientation des actions
d’amélioration et à une mobilisation de moyens parfois plus
importants que nécessaire pour agir sur des critères importants en
logique, au détriment d’autres facteurs plus faciles à maîtriser
mais classés logiquement en points mineurs.
Ces écueils et la généralisation dans les logiciels de traitement d’enquêtes des méthodes de calcul automatique de l’importance des critères font qu’il est rare aujourd’hui de procéder par cette méthode déclarative. Les alternatives imposent toutefois, comme nous allons le voir ci-dessous, quelques règles dans la structuration du questionnaire.
La régression multiple
Il s’agit de l’une des méthodes les plus connues pour expliquer une variable dépendante par plusieurs variables indépendantes. Elle est d’un accès plutôt facile et est proposée sous différentes formes dans la plupart des outils statistiques du marché.
Nous l’évoquons ici en préambule des méthodes calculatoires d’évaluation de l’importance des critères de satisfaction tout en précisant que la méthode souffre de certaines limites qui la rendent peu applicable dans le cadre d’une évaluation opérationnelle de l’importance des différents facteurs dans les enquêtes de satisfaction. Voyons d’abord son fonctionnement avant de préciser ce qui nous amène à lui préférer les deux autres méthodes détaillées plus loin.
La régression multiple est une opération qui aboutit à la modélisation d’une équation de la forme : Y = a1X1 + a2X2 +… + anXn + u
Y est la variable à expliquer et X1 à Xn les variables explicatives. Les valeurs a1 à n sont des coefficients calculés et u le résidu.
En appliquant une régression multiple pour expliquer une variable de satisfaction globale (SAT) par un ensemble de 5 critères (C1 à C5), on obtient une formule du type : SAT = 0,3C1 + 0,5C2 + 0,1C3 – 0,05C4 + 0,8C5 + 0,13
Cette équation modélise la satisfaction globale en nous indiquant une priorité d’action importante, C5, qui agit davantage lorsqu’on l’augmente sur la satisfaction globale que, par exemple, la variable C3. On peut voir également que l’amélioration de la satisfaction sur le critère C4 est censée faire baisser la satisfaction globale.
On perçoit déjà ici l’un des problèmes de la régression multiple
qui peut donner dans certains cas des coefficients négatifs difficiles à
interpréter. Les autres limites sont les suivantes :
- Le calcul de la régression multiple se base sur des variables
numériques. Or les questions de satisfaction ont recours le plus souvent
à des échelles en 4 points qui hiérarchisent les réponses sans
introduire véritablement de notion de distance (la réponse « très
satisfait » n’est pas obligatoirement aussi éloignée dans
l’esprit du répondant de « satisfait » que cette dernière ne
l’est de « peu satisfait »). Une utilisation sur une échelle en 4
points peut aboutir à des résultats peu concluants. Elle exige
d’ailleurs le plus souvent d’inverser le codage en utilisant
des valeurs de 4 à 1 ou des coefficients comme [10, 7, 4 et 1] plutôt
que la position des modalités de 1 à 4 afin de disposer plus logiquement
d’une satisfaction forte plus élevée que la satisfaction
faible.
- Le calcul de la régression multiple ne fonctionne, par définition,
qu’avec des variables explicatives indépendantes,
c’est-à-dire peu corrélées entre elles. Or c’est rarement le
cas dans les enquêtes de satisfaction où l’on propose généralement
des batteries de critères dont plusieurs se recoupent ou présentent une
forte dépendance. Il est donc fréquent que votre logiciel statistique
vous indique que le calcul est impossible pour le jeu des variables
choisies. Le risque est d’ailleurs d’autant plus grand que
le nombre de critères est important.
- Même lorsque les conditions sont réunies pour que la régression
s’exécute, il est nécessaire d’observer les indicateurs
statistiques fournis pour s’assurer de la validité de l’
(R², résidus…).
Suite à un calcul de régression, il est possible de traduire les résultats en un mapping qui présentera en abscisse les notes de satisfaction et en ordonnée les coefficients de corrélation entre chaque variable et la variable de satisfaction globale. On se retrouve donc avec une matrice que l’on peut prendre en compte en oubliant les limites ci-dessus, pour ne se focaliser sur l’interprétation des résultats. Nous vous conseillons donc vivement, avec les matrices issues de régressions, de vérifier les bases statistiques et de manipuler les résultats avec précaution. Le mieux reste encore de préférer les autres méthodes exposées ci-dessous qui font appel à l’analyse factorielle et sont plus robustes et moins sensibles aux biais.
La méthode Satimix
Cette méthode a été mise au point il y a déjà une vingtaine d’années par Jean-François Grimmer, statisticien et concepteur d’un logiciel d’analyse de données. La méthode a fait l’objet d’une publication dans la Revue Française du Marketing en décembre 93 en se basant sur l’exemple des enquêtes de satisfaction d’EDF-GDF Services.
La méthode Satimix repose sur un modèle multi-attributs qui vise à expliquer la satisfaction globale par les différentes dimensions élémentaires évaluées. Le pré-requis de cette méthode consiste donc à prévoir impérativement dans le questionnaire une question de satisfaction globale et d’utiliser, pour les critères de satisfaction évalués, la même échelle de notation que pour cette question d’ensemble. L’idéal est d’utiliser une échelle en quatre points (très satisfait, assez satisfait, peu satisfait et pas du tout satisfait).
Dans ses calculs, Satimix cherche à déterminer les variables les plus contributives à la satisfaction globale. Pour cela, la méthode regroupe les modalités en trois groupes de niveau de satisfaction : FORT, MOYEN et FAIBLE. Dans le cadre d’une échelle en quatre points, les deux premiers sont pris tels quels et les deux derniers sont regroupés dans la rubrique FAIBLE, pour remédier à la faiblesse d’effectifs qu’on y observe généralement.
Satimix a pour objectif de calculer l’effort à accomplir pour passer du niveau de satisfaction moyen au niveau de satisfaction élevée, pour aboutir à une amélioration de la qualité de service. Dans certains cas où les niveaux de satisfaction sont vraiment faibles, on peut viser plus simplement à éliminer les « points noirs ». On cherchera alors à connaître l’effort à faire pour passer du niveau faible au niveau moyen. Logiquement, chacun de ces deux objectifs doit aboutir à une évaluation différente de l’importance à porter à chaque facteur, et par conséquent à une répartition différente des critères dans la matrice importance-satisfaction. On peut donc se retrouver, avec les mêmes données et la même méthode avec deux configurations complètement différentes, d’où l’importance de bien identifier les paramètres demandés, surtout s’il s’agit de faire des comparaisons d’évolution des résultats dans le temps .
Pour mesurer l’association entre les différentes variables, Satimix utilise le Khi², de préférence au coefficient de corrélation. La première étape du calcul consiste à préparer un tableau de contingence présentant les 3 modalités de la satisfaction globale en colonne et 3 lignes par critère de satisfaction partielle. Une analyse factorielle des correspondances est appliquée sur ce tableau et permet d’obtenir une projection sur un même axe des critères détaillés de la satisfaction avec la question de satisfaction globale. Chaque point correspond à l’une des 3 modalités Fort, Moyen et Faible de chaque variable de satisfaction, y compris la satisfaction globale. On constate généralement que les trois nuages de points regroupant les items pour chacun des trois niveaux sont disposés dans l’ordre d’importance décroissante, de gauche à droite sur l’axe horizontal. On considère alors que cet axe représente le niveau de satisfaction.
Pour évaluer l’importance des facteurs, le système s’intéresse à l’écart pour chaque critère entre le point MOYEN et le point FORT. Autrement dit, on cherche à calculer l’effort que doivent faire les personnes ayant donné la réponse « Assez satisfaits » pour atteindre le point idéal que constitue la réponse « Très satisfaits ». Bien entendu, on raisonne ici sur l’ensemble des répondants et non sur chacun d’entre eux. Cet écart sur les coordonnées factorielles est ensuite pondéré par le nombre d’individus concernés pour affiner et compléter le calcul de l’importance.
Comme on peut le constater, cette méthode qui passe par de multiples opérations statistiques ne peut être effectuée manuellement. Sur le marché, les principaux logiciels d’enquêtes (comme par exemple Ethnos avec son module d’analyse de données Stat’Mania) permettent de calculer et d’obtenir directement la matrice d’importance-satisfaction, à partir de la simple indication de la variable de satisfaction globale et des variables explicatives que vous souhaitez utiliser.
L’analyse Tétraclasse
Ce modèle que l’on doit à la chercheuse française Sylvie Llosa de l’IAE Aix-Marseille est dit asymétrique dans la mesure où il part du postulat qu’en matière de satisfaction, les critères contribuent de façon variable à la satisfaction globale. Certains d’entre eux agissent positivement sur la satisfaction alors que d’autres interviennent principalement sur l’insatisfaction. Ainsi, une réduction ou un petit cadeau offert en caisse alors que vous ne vous y attendiez pas peut générer chez vous une satisfaction particulière. En revanche l’absence de ce cadeau inattendu ne provoque pas d’insatisfaction particulière. A l’inverse, des facteurs négatifs comme par exemple la présence d’obstacles dans les rayons d’un magasin peuvent aiguiser votre insatisfaction. L’absence de ces obstacles logiquement improbables n’est pas en soi un motif de satisfaction particulière.
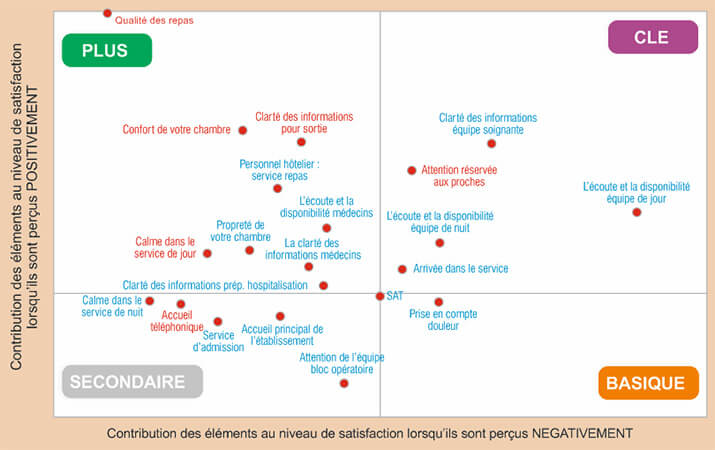
Le graphe montre notamment que, pour les patients en chirurgie, un seul élément est basique : la prise en compte de la douleur. Une mauvaise évaluation de ce critère entraîne une forte insatisfaction alors qu’une bonne évaluation n’augmente pas fortement la satisfaction. Les éléments « clés » regroupent les critères liés à l’équipe soignante, tandis que les éléments « plus » concernent surtout les aspects liés à l’activité hôtelière et que les éléments « secondaires » sont surtout administratifs.
Cette approche asymétrique s’oppose donc à la conception habituelle d’une influence quasi linéaire de la satisfaction des facteurs sur la satisfaction globale. Ici, on ne considère donc pas que plus un critère est satisfaisant plus il a d’influence sur la satisfaction globale et inversement, même si on continue à admettre que certains éléments essentiels peuvent avoir une influence dans les deux sens.
Le modèle Tétraclasse a pour objectif d’évaluer la variabilité de
la contribution des différents facteurs et d’identifier
d’une manière qui se veut plus fiable les éléments prioritaires à
améliorer pour accroître la satisfaction globale. Dans le même temps, la
méthode facilite l’identification d’éventuels critères de
sur-qualité, qui génèrent des dépenses inutiles sans intervenir
valablement sur le niveau de satisfaction. La méthode distingue pour
cela quatre catégories d’éléments :
- Les critères « basiques » : il s’agit de critères dont la
mauvaise performance fait fortement baisser la satisfaction globale mais
dont la bonne performance n’a que peu d’effet sur
l’amélioration de cette satisfaction.
- Des critères qui apportent un surcroît de satisfaction
lorsqu’ils sont évalués positivement mais qui n’entraînent
pas d’insatisfaction d’ensemble lorsqu’ils sont moins
bien notés.
- Les critères « clés » : éléments qui contribuent de façon
importante à la satisfaction globale quelle que soit l’évaluation.
Ils augmentent la satisfaction lorsque les attentes sont dépassées et
génèrent de l’insatisfaction en deçà.
Les critères « secondaires » : éléments qui contribuent faiblement à
la satisfaction globale qu’ils soient évalués positivement ou
négativement.
La méthode Tétraclasse exige exactement la même structure de questionnaire que dans le modèle Satimix : une question de satisfaction globale et un ensemble de critères de satisfaction, avec, pour chaque critère, une même échelle d’évaluation (en 4 positions de préférence ou bien une note sur 10). Le mode opératoire de l’analyse commence par une dichotomisation des modalités, en regroupant d’une part les 2 éléments positifs (+) et de l’autre les 2 éléments négatifs (-). Comme dans Satimix, la méthode établit un tableau de contingence de 2 colonnes SATI + et SATI – (au lieu de 3 dans Satimix) et du nombre de critères x 2 en ligne, puisqu’on considère pour chaque critère la rubrique positive et la rubrique négative.
Le calcul se poursuit, comme dans Satimix, par la production d’une AFC sur la base de ce tableau, qui génère deux coordonnées pour chaque élément. En partant d’un tableau à 2 colonnes, on obtient des points, tous représentés sur un même axe. Cet axe factoriel est explicatif de 100% de la variance des données prise en compte. On peut considérer qu’il s’agit de l’axe de la satisfaction. On y retrouve le point SATI + de satisfaction globale positive et SATI – de satisfaction globale négative. Y figurent également pour chaque critère étudié les deux modalités de satisfaction positive et négative. Plus un critère figure aux extrémités de cet axe, plus il contribue positivement ou négativement à la satisfaction globale.
C’est là qu’intervient l’idée originale et très efficace de Llosa, qui a imaginé de procéder à un « pliage » de l’axe pour permettre une visualisation sur un mapping des différents points. Il suffit pour cela de garder pour chaque point la coordonnée négative en abscisse mais d’utiliser la coordonnée positive en ordonnée. Pour faciliter la lecture, on effectue un centrage sur le point de satisfaction globale qui a les coordonnées de SATI – en abscisse et de SATI+ en ordonnée (et qui est donc ramené à 0,0). Le résultat est un mapping en 4 cadrans, qui propose en haut à gauche les critères PLUS, en haut à droite les critères CLE, en bas à droite les critères de la catégorie BASIQUE et en bas à gauche les critères de type SECONDAIRE.
Les méthodes Satimix et Tétraclass aboutissent donc toutes les deux à un mapping des critères, avec des approches différentes mais complémentaires. Il vous est d’ailleurs possible en partant du même jeu de données, d’appliquer les deux analyses et de comparer les résultats, si votre logiciel intègre les deux méthodes (c’est le cas d’Ethnos/Stat’Mania).














