With a distribution tabulation of a range of variables or crossed
variables, the survey responsible person tries to evaluate the obtained
information meaning. To do this, he uses a large sample of statistical
test in order to choose those that match with her aims. This file
describes the main utilizable test for surveys and details their aims
and their launching mode. Statistical tests especially enable to
evaluate the obtained distribution in order to know whether they are due
to chance or they hold interesting information.
Fisher, Kendall, Student, Pearson... Many known names of people having
used statistics and probabilities. Hypothesis tests linked to these
mathematician or statistician names are today widely used in many
research fields in order to evaluate the meaning of the obtained
observations. In the marketing surveys universe, only some tests such as
the one from the Khi2 are often used. As we are going to learn, other
available tests can also be really useful for surveys responsible
people.
Main principles
Aims
It exists many tests that enable to evaluate different aspects of the significance. The main aims to which statistical tests can deal with are:
- The representativeness evaluation of the of the observed distributions
compared to the known values for the whole population
- The representativeness measurement of the observed differences
about the observations of two groups of individuals or of one same group
for two observed variables, the existence and the intensity of a bond
between two variables.
Functioning
The statistical tests work according to the same principle that consists
in formulating a hypothesis concerning the parent population and then
check it with the noticed observations whether they are likely in this
hypothesis case. In another way, we try to estimate the probability of
then random draw in the parent-population from a sample having the
observed characteristics. If this probability is negligible we reject
the observed hypothesis; conversely if this probability is huge, the
hypothesis can be adopted (at least temporarily) in the wait for further
validation. The hypothesis to be tested is called HO or null hypothesis.
It is always accompanied by its alternative hypothesis called H.
The test will validate or reject HO (and so it will make the invers
conclusion for H1). If the result of the test brings to accept the null
hypothesis H0, the survey responsible person deducts that she cannot
conclude anything from the concerned observations (the probability of
distribution due to chance is huge). However, the reject of H0 means
that the distribution of the answers holds particular information that
does not seem to be due to chance and that are needed to be deepened.
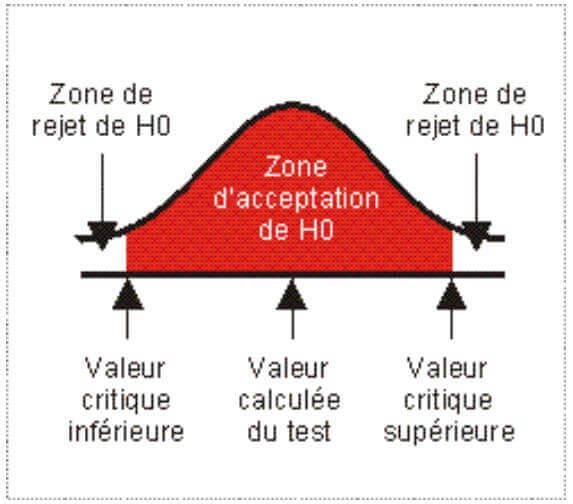
Utilization mode
The launching of a statistical test usually takes place in 5 steps:
- The formulation of the null hypothesis H0 and of its alternative
hypothesis H1: these hypotheses are always formulated compared to the
global population while the test will concern the observations made for
the sample.
- Example: Compared to last year when our customers gave a 8,7 out
of 10 note for our store, the given note this year by 100 interviewed
customers is around 8,5/10, which is not this much less.
- Establishing the meaning threshold of the test (called alpha and
explained further).
Example: we accept a unique error risk of 5%.
- In the parametric tests case (definition to come further),
determination of the probability law that matches to the
parent-population.
Example: if we interrogate all our potential customers, the given note
would be divided up a normal distribution with a standard deviation of
1.
- Calculation of the reject threshold of H0 in order to determinate
the reject area and the acceptance area of H0 (and conversely of
H1).
Example: For a 5% risk, the normal rule gives a critical value of
-0,1645. If the value of our test is higher than this threshold, our H0
hypothesis is verified: the note of this year is not this much inferior.
- Decision of rejecting or of acceptance of the H0 hypothesis.
Example: the comparison of the difference between 8,5 and 8,7 that is
-0,2, being inferior to the critical value, we have to reject the H0
hypothesis. So we have to estimate that the given note of this year is
significantly inferior to the one of last year.
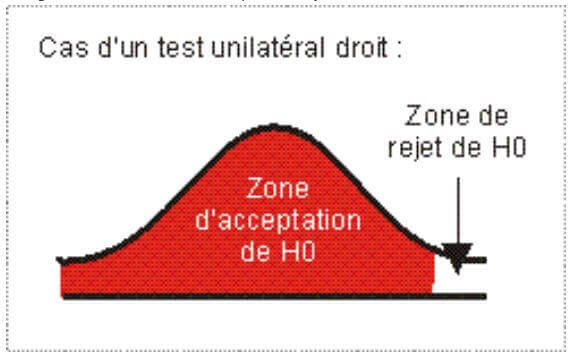
Unilateral or bilateral test
When the null hypothesis consists in testing the equality of the test
value with a given value, the test is bilateral. Actually, the reject of
the hypothesis is decided whether the test value is significantly
different, even it is inferior (link reject area) or superior (right
reject area). The test is said unilateral when the null hypothesis
checks if a value is superior or equal to the test value (link
unilateral) or inferior or equal to this value (right unilateral).
The given test in the above example actually is a link unilateral test.
Parametric and not parametric tests
We distinguish two huge categories of tests: parametric tests and not
parametric tests. Parametric tests need the distribution form of the
analyzed parent-population to be specified. For example, it can be a
distribution following the normal rule, which is generally the case when
we deal with huge samples. Usually, these tests are only applicable for
numerical variables.
Not parametric tests are applicable both for numerical and qualitative
variables. These tests do not refer to a particular distribution of the
parent-population. They can be used for small samples.
Theoretically, they are less powerful than the parametric tests but we
can consider that not parametric tests are more convenient to surveys
issues. Surveys have proved that their precision on huge samples is just
a little bit inferior to the one of the parametric tests while they are
extremely more exacts on small samples.
Standard errors
The retained conclusion (reject or not reject of the H0 hypothesis) is
established with some error probability.
When the test conducts to the reject of the null hypothesis, the
eventual error is « Type 1 error » or « Alpha error » when this
hypothesis is actually true. In the above example, the alpha error was
fixed to 5%.
Conversely, when the test tells us that the hypothesis does not need to
be rejected, the eventual error when this hypothesis would actually be
false is called « Type 2 error » or « Beta error ».
These indicators are interdependent: when the alpha error is reduced,
the beta error increases. This means that the choice of the alpha
threshold for the test to be made must be chosen according the economic
cost of one or another bad decision.
Example: Before launching a new packaging, a company performs a test to
check if it is more likable by the customers than the old one.
Whether the hypotheses are verified while it was false, the company will
replace the old packaging that is more liked by the new one that is less
attractive. The company is going to lose money and customers. However,
if the test indicates that the new packaging is less tempting while it
actually is more tempting, the company will lose an opportunity by not
launching the new packaging. Comparison of the costs of these two errors
enables to fix the thresholds in a more optimal way. Let us notice that
the alpha and beta indicators enable to formalize a safety level for the
obtained result (1 –alpha) and a parameter indicating the power of the
test (1 –beta).
Testing a variable
The production of a results table about a question can be accompanied by significance statistical indicators. The choice of the practicable test depends on the type of the variable and of the pursued aim.
Harmony tests
With a results table for a qualitative variable, the survey responsible
person can use not parametric tests intended to compare the obtained
distribution for the different answers with a known distribution (for
example: the one of the parent-population) or a theoretical
distribution, coming from a statistical rule (ex: the normal law).
The two most used harmony tests in this case are the adjustment test of
the Khi2 and the Kolmogorov-Smirnov test.
These tests enable to answer such questions:
- I know the distribution of my population according the CSP. Is my
sample representative of this population according this criterion?
- We defined a charge plan enabling us to open our cash desks
according to our store visits. Does this model fit with our observations
on a given sample of days and hours?
- We produce shoes for women. Can we consider than the sizes follow
a normal law after we interrogated 200 potential customers chosen by
chance?
- These tests calculate a value (from the distance between the real
values and the theoretical values), that we compare to a critical
threshold in the matching statistical tabulation.
Conformity tests to a standard
These tests are close to harmony tests mentioned above. Their aim is to
compare an average or a proportion to a particular value (as in our
example from the beginning). The comparison test of the average is used
on a numerical variable and enables to compare the average of the set to
a given value. This is only utilizable for a sample higher than 30
individuals.
In order to bring a new picture of this test utility, let us see the
example of a magazine that affirms that each sold magazine is read by an
average of 3,7 readers in order to sell its advertisement pages. The
comparison of the average enable to evaluate the truth of this
affirmation thanks to the random sample of interviewed people. The test
does not only consist in comparing the obtained average, for example
3,2, with the announced average but also to estimate the probability to
find a sample with an average that move from 0,5 points or more compared
to the real average of 3,7. Whether this probability is huge, we can
accept the announced average. However, if it is negligible, we can
reject the affirmation.
The comparison test of proportion woks on the same way, but on
qualitative variables. It enables to compare the percentage of obtained
answers for a modality to a given percentage.
Whether an antenna manager fixed a minimum of 25% threshold of auditors
in order to keep a TV show and that she obtains the value of 22,5% of
auditors after a survey, the comparison test of the obtained proportion
with the wished threshold can help her to take a decision minimizing the
risk to make an error.
Tests on two variables
Parametric tests of sample comparisons
These tests enable to compare obtained results for a variable on two
observation groups, in order to determine whether these results are
significantly different from a group to another one.
It can be a test of two packagings or two advertisement messages for
example, in order to evaluate the most liked version by the interviewed
people.
The most usual parametric tests of comparison are the difference tests
between two averages or between two percentages.
The first one is applicable for numerical variables. It can be used on
independent or paired samples.
Here is an example: if we make a women group and a men group tasting a
drink in order to see if an estimation difference stands according to
the sex, then we make a test on independent samples.
However, if we make a same individuals group tasting two different
drinks, in order to know if a significant difference stands for one
drink, we make a measurement on paired samples.
In the first case, the test compares the average for the 1st and the 2nd
group and then tries to evaluate whether this difference significantly
is different from 0. If it is the case, we can consider that men do not
like the drink in the same way than women. In order to know which group
like it the most, there is no need for the test to be made in a
unilateral way because it only need to have a look on the averages.
In the second case, the test consists in calculating the differences
between the two given notes by each individual for the tasted product.
Then the test calculates the average of these differences and tries to
see whether this average significantly is different from 0. If it is the
case, we can conclude that the products are evaluated in a different
way. The judgment of the best product can be made by an exam of the
average of each product or by asking a unilateral test at the
beginning.
The comparison test of two percentages also is extremely useful in order
to evaluate the difference between two samples for a given answer
modality (or a group of the modality). A big distribution brand can
compare the proportion of satisfied customers in two of its stores in
order to know if this difference is significant.
Non parametric tests of samples comparisons
These tests have the same objectives than their parametric counterparts
by being applicable in the general case.
The U test of Mann-Whitney is similar to the comparison test of the
averages on two independent samples. As this test, the U test applies on
a numerical variable (or ordinal qualitative).
The signed-rank of Wilcoxon is also similar to the comparison test of
the averages but on paired samples. The two variables to be tested must
be numerical (or assimilated).
These tests make rankings of the answers and use the associated rank in
their calculations.
The Mann-Whitney test begins to link the answers of the 2 X and Y groups
together and to classify them. The calculation is in relation to the
time an individual of the W group get ahead a Y group individual. The
sum of these elements enables to obtain the test value to be compared to
the critical value in the Mann-Whitney table.
It exists another non parametric test enabling to compare more than 2
samples and that actually is the generalization of the Mann-Whitney
test. It is the Kruskal-Wallis test.
Measurement of the association of two qualitative variables
The meeting of these two qualitative questions produces a table that we
also name “eventuality table”.
To know if the answers distribution of these two variables is due to
chance or if it reveals a link between them we usually use the Khi2 test
that probably is the most known statistical test and the most used in
the marketing surveys field. A box in this document details its
functioning.
Generally, the Khi2 is calculated for a crossed table. However, some
tools such as Stat’Mania are able to apply it in set to a many variables
combinations that are taken 2 by 2 in order to automatically detect
variables couples that present the most significant links.
Measurement of the meeting of two numerical variables
When we try to determinate if two numerical variables are linked we talk about correlation.
The three most used correlation tests are the Spearman, the Kendall and the Pearson tests.
The two first tests are non-parametric tests that can also be used on
ordinal qualitative variables.
These two tests start by classifying the observed values for each
individual for each of these two variables.
So if we try to evaluate the correlation between the age and the income,
the first calculation step makes the evaluation for the 1 individual,
the 2 individual and then the n individual, its ranking is made
according to the age and the income of the individual.
The Spearman test is based on the difference between ranks for each
individual in order to give to each individual the test value (r of
Spearman), from a particular formula. More is this value close to 0,
more are the 2 variables independents. Conversely, more is the value
close to 1, more are the 2 variables correlated.
It is possible to test the statistical significance of this obtained
value with the help of this comparison formula, based on the t of
Student:
t = RxRoot(n-2) / Root(1-r²)
This value must be compared in a Student table, at the t value with n-2
liberty degrees. If we obtain a r value of 0,8 on a 30 people sample,
the above calculation gives us the 8,53 value. The given value in the
Student table for 28 liberty degrees with a 5% error threshold is 2,05.
This value is inferior to our calculated t, the calculated correlation
rate is significant.
All these operations are, of course, assured in an automatically way by
all the modern software of data analysis (for example STAT’Mania).
The Kendall test begins the same way than the Spearman test. But once the
ranks are calculated, the test classifies these two variables on these
ranks and is interested in the time the second one respects the same
ranking order.
Finally, the test gives a correlation rating that is called the Tau of
Kendall of which we also can calculate the significance with the help of
an additional test.
Conversely to these two above tests, the Pearson correlation test is a
challenging parametric test. It can only be used on two numerical
variables that must follow the normal law when they are used together
(it is complicated to verify in the marketing surveys).
This correlation test uses statistical calculations based on the
covariance of these two variables and their variance.
These calculations also end on the production of a correlation rating
between 0 and 1 that can also be tested for its significance.














