What is the multi-varied analysis?

The multi-varied analysis covers a set of methods aimed to summarize the information coming from several variables, in order to explain it in a better way. There are two huge categories of methods: the descriptive methods and the explanatory methods.

The descriptive methods

These methods try to structure and simplify data coming from several variables without particularly favoring one of them. The most used methods in the surveys treatment are:

- The principal component analysis (PCA)
- The factorial correspondence analysis (FCA)
- The multiple correspondence analysis (MCA)
- The typology and classification methods

The choice of one or another method depends on the pursued goals and on the kind of data to be analyzed. Stated methods are detailed in the next pages.

The principal component analysis

The PCA covers a set of digital variables. It enables to position individuals on a two-dimensional plan, according to the proximity of their answers to chosen questions. Variables are also represented on the mapping, but in an independent way from the individuals-points.
The PCA enables to highlight the answers structure by showing the individuals group according to answers combinations to the chosen questions.
The mapping axis usually do not match with one or another variable but with an optimal group of several variables (ex: income and study level can be a part of an axis starting in a way where they really can be correlated).
PCA is really useful when we work on a statistical limited and identified set of individuals.
So, if we want to analyze sales points according to different digital criteria (surface area, employees, turnover, sold pieces number…), the PCA enables to obtain an interesting map that join sales points according all retained criteria and that also enables to categorize them and especially to identify the nonstandard cases (ex: important surface area with many employees but low turnover…).
The start table of the PCA contains online individuals and variables in the rows, with, for each case, the digital response of the individual to the matching question. Ordinal qualitative questions, the ones for which answers can be ordinal organized between them (scales, frequencies…) can be codified again in order to enter the PCA table. This recodification must be prepared in advance. However, some statistical analysis software such as STAT’Mania enable to make this recodification in live, during the choice of the variables that should enter the PCA. The PCA algorithm performs some different operations on the individuals/variables matrix (data adjusting-decrease, diagonal of the matrix, extraction of the data and vectors…) in order to go from the initial number of variables to a small number of variables obtained by the combination with the first ones.
These new elements constitute the mapping axis. The first element is the one which summarize well contained information in the table. The second element brings an inferior percentage but with complementary information, and so on.
The PCA mapping firstly represents the first element (the horizontal axis) and the second one (the vertical axis). Sum of explanation percentages of the two elements tells us about the information loss rate from basis data. So, the first element sums up 62% of the table and the second one sums up 21%. The represented information on the mapping has a rate of 83%. The “lost” information actually is 17%.
The individuals-points are represented on the mapping according to their contact details on the factors. A priori, the close points are individuals with close profiles, according to the answers to the chosen variables in the analysis.
The variables-points also are represented on the mapping, but completely independent from the individuals.
Their representation shows the correlation with factors inside a 1 radius circle defined with an arbitrary scale (that can be changed as we want without affecting the individuals-points representation).
These variables-points tell us about the sense to give to the axes. So, a variable close to the correlation circle (high correlation) and close to an axis contributes a lot to the start of this axis.
Inter-variables angles (from the origin) tell us about correlation between them. So, two variables that form a small angle are highly correlated while a right angle would mean that they are independents.

Choosing a multi-varied analysis method

Different multi-varied analysis methods enable to answer to multiple problems. The choice of one method depends on the initial objective, on the manipulated variables types but also on the obtained results form that can be more or less easy to present and to explain.

In order to intuitively understand

The multi-varied analysis tries to sum up the data coming from several variables by minimizing the loss of information. In order to understand well what it means, let us take the example of PCA that is applicable on three digital variables or more.
When we have two digital variables, for instance the age and the size, it is easy to imagine a graphical representation that reproduces all the information: a two axes graphic, one for the age and the other for the size, and a position of each individual-point according to her values for each of the two variables.
If we add a third variable, for instance the number of children, we would need a three dimensions graphic, which is more difficult to read.
By adding a fourth variable, for instance the income, we pass the limits of what the human brain is able to visually comprehend.
An analysis such as the PCA brings the points cloud in three, four or n dimensions to a two dimensions plan.
However, the chose axes do not match to one or another variable but are virtual axes coming from combinations between variables and calculated to move as closer as possible from all the cloud points. Each point is rejected on this plan. The combination of distances of each points compared to the determined plan corresponds with the volume of lost information.
The multi-varied analyses have a set of indicators that enable to determine this level of missing information and to decide the relevance or not of the obtained results and the necessity of deepen the analysis by using complementary digital tables and displays of data on other angles.
So, if the two first axes of a PCA do not five a crushing part of the information, it is needed to get interested in the additional information given by the third axis. For that, we can ask to display the plan formed by the 1 and 3 axes and the one of the 2 and 3 axes. We can also read details of the different points for the different axes in the table in order to find eventual important gaps (two points side by side on the main plan can be actually far from each other).

How to read a PCA ?

Below explanations come from a PCA realized with the STAT’Mania software. The example is about an analysis of a number of criteria about stores located in several towns. Successive questions to ask are:

How many axes are interesting for our analysis?

To answer this question, we need to consult the table of the eigenvalues, wich always come with the PCA.

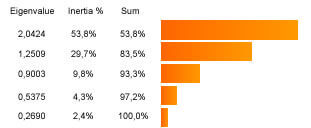
There are two different ways to determine the number of axes to take into account:

- An “absolute” criterion: only keep axes with eigenvalues that are superior to 1 (this is the Kaiser case).
- A “relative” criterion: only keep eigenvalues that “prevail” on the others by referring to the screeplot of the values.

It is necessary that the retained eigenvalues reproduce a “good proportion” of the analysis. This means that the sum of the inertia explained by each axis (3 columns) represents an important part of the total inertia. This sum is a measurement of the reliability of the mappings reading and so, of the global explanatory quality of the analysis.

In what points are we interested ?

The most interesting points usually are those that are close enough to one of the axes and far enough from the origin. These points are well correlated to this axis and are the explanatory points for the axis: these are the most “speaking” points; their “real distance” from the origin is well represented on the factorial plan.
In the below mapping, we clearly see that Nice is extremely correlated to the horizontal axis. Likewise, Paris and Reims are particularly well correlated to the vertical axis. The correlation of each point on an axis expresses the representation quality of the point on the axis. It takes values between 0 (not correlated at all) and 1 (highly correlated). If this value is close to 1, the point is well represented on the axis.

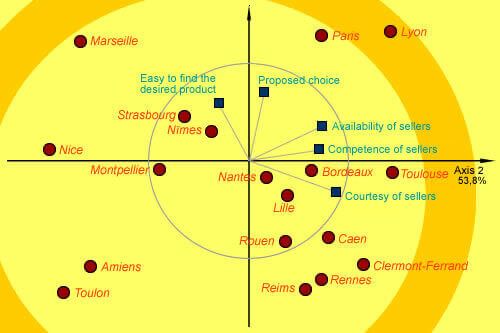
Points located near the center usually are badly represented by the factorial plan. Their reading cannot be faithfully made.

How to interpret proximities ?

We essentially are interested in well represented points (i.e. located far from the center). Whether two points are close to each other, it is possible that the individuals’ answers that they represent are really similar. However, we need to be careful: it is possible that they are really close on an axis while they will be really far on another one. We must look at them compared to all axes that were retained for the analysis. Whether they are well correlated to the axis that shows them the closest, we can conclude that they are really close.

Can we give a “real” sense to mapping axes ?

Factorial axes are virtual axes coming from a synthesis between the variables of the analysis. They not necessarily have a precise sense even if we can often find them a sense with the help of the variables representation on the correlation circle. Do not forget that the representation of this circle and of the variables on the PCA mapping is made according to an arbitrary scale, which involves that the variables-points proximity compared to the individuals-points does not make any sense.

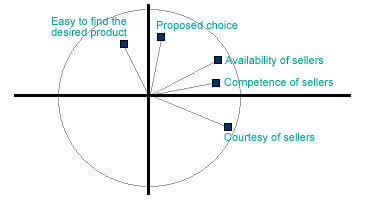
In our example, we can notice that “availability”, “competence” and “courtesy” points are really close to the correlation circle and so, well represented on the mapping. The almost closed angle (going from the origin) that is formed by the “competence” and “availability” points indicates that these 2 variables are quite well correlated to each other. However, the almost right angle formed by “competence” and “choice” indicates that these 2 variables are independents to each other.
The fact that “competence” is close to the 1 axis tells that it is really well represented by this axis. Because it is really far from the 2 axis, we can conclude that it is not much represented by this axis.
Concerning the 2 axis, the “choice” point is really well correlated to the axis. The “facility” point is also well correlated but in a fewer measurement.
From these observations, we can conclude that the 1 axis rather matches with the appreciation of sellers and especially of their competences whereas the 2 axis rather matches with the appreciation of the store and especially of the choice that it proposes.
By summarizing the information coming from the 5 analyzed variables, our mapping shows us that there are a lot of efforts to do concerning the welcoming and the information for the customers in the stores in Nice, Marseille, Amiens and Toulon. Toulon is also few liked in terms of choices.
Stores of Paris, Lyon and Marseille are liked by the customers for the choice they offer and the facility to find the wished products.
Lyon distinguishes itself with the kindness of the employees and can be considered as the best store within those that were analyzed. These conclusions are confirmed by the examination of the correlations tables and the individuals’ details, given by the analysis software.